Exercices Droites, plans et vecteurs de l'espace

Voici une figure représentant un cube de côté $1$ :

On considère :

• $U$ le milieu de $[HG]$ ;
• $K$ le milieu de $[FG]$ ;
• $Y$ le milieu de $[EC]$.

Parmi les points $Y$, $U$, $K$, $F$, lesquels sont équidistants de $E$ et $C$ ?

On considère un cube $ABCDEFGH$ et on note :

$I$ et $J$ les milieux respectifs des segments $[AB]$ et $[BC]$ ;
$K$ le point d’intersection des droites $(IJ)$ et $()CD$ ;
$L$ le centre de la face $ABCD$.

Représenter par une figure la situation de l’énoncé.

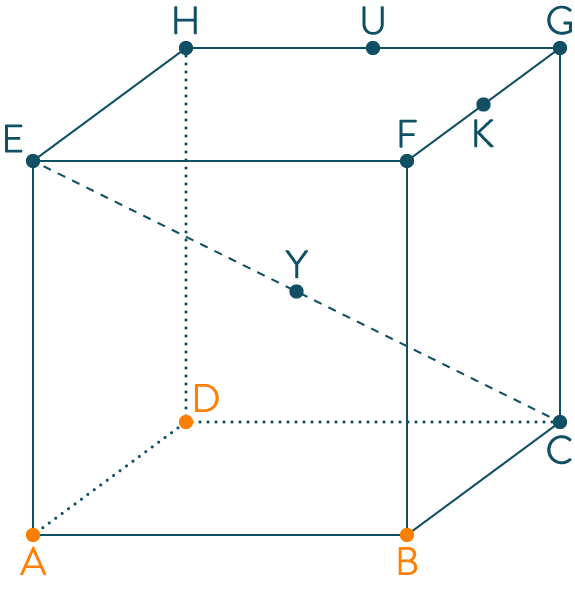
Dans l’espace, on considère le tétraèdre $SABC$ représenté ci-dessous. $F$ et $G$ sont les milieux respectifs des arêtes $[AB]$ et $[AS]$.

On considère par ailleurs :

• le point $L$ tel que :

$$\overrightarrow{AL\ }=\dfrac 12\cdot \overrightarrow{AC\ }+\dfrac 12\cdot \overrightarrow{AS\ }$$

• et $O$ le point défini par l’égalité vectorielle :

$$\begin{aligned} &\overrightarrow{OA\ }+\overrightarrow{OB\ }+\overrightarrow{OC\ }+\overrightarrow{OS\ }=\vec 0 \\ &\footnotesize{\textcolor{#A9A9A9}{\text{où $\vec 0$ est le vecteur nul}}} \end{aligned}$$

• $O$ est appelé centre de gravité du tétraèdre $SABC$.

Question 1

Reproduire le tétraèdre sans souci d'échelle et y placer le point $L$.
Montrer que $L$ est le milieu de l’arête $[SC]$.

Question 2

Démontrer que $\overrightarrow{AO\ }=\dfrac 14\cdot (\overrightarrow{AB\ }+\overrightarrow{AC\ }+\overrightarrow{AS\ })$.

Question 3

Justifier que $(\overrightarrow{AB\ },\,\overrightarrow{AC\ },\,\overrightarrow{AS\ })$ forme une base de l’espace.

• Dans la suite, on munit l’espace du repère $(A\ ;\, \overrightarrow{AB\ },\,\overrightarrow{AC\ },\,\overrightarrow{AS\ })$.

Question 4

• Déterminer les coordonnées des points $F$, $G$, $L$ et $O$ dans le repère $(A\ ;\, \overrightarrow{AB\ },\,\overrightarrow{AC\ },\,\overrightarrow{AS\ })$.
• Les points $F$, $G$ et $L$ sont-ils alignés ? Justifier votre réponse.
• Calculer les coordonnées du milieu de $[FL]$.
  En déduire que les points $F$, $G$, $L$ et $O$ sont coplanaires.
• Représenter le point $O$ sur la figure.